Recursion (Part 1)

Revisiting helper functions

We've seen how useful it is to be able to write functions using helper functions, coming up with a “wish list” of functions it would be nice to have to solve a problem.

That is, we break a task into subtasks, break subtasks into further subtasks, as appropriate, and when there are no built-in functions to do the job, we create helper functions. So here's a conundrum: what if the most useful possible helper function is precisely the function that we are in the process of writing?

Example: factorial

For example, suppose we wished to compute a factorial. This is the product of a number, one less than the number, two less than the number, and so on down to 1. For example, 5 factorial is 5 × 4 × 3 × 2 × 1.

---

To compute 5 factorial, we can multiply 5 by 4 factorial, since 4 factorial is the product 4 times 3 times 2 times 1. So, the best helper function to compute a factorial is a function that computes a factorial.

---

Example: Fibonacci numbers

As another example, suppose we wished to calculate a Fibonnaci number. This is a sequence of numbers that appears in nature in many settings. The first two numbers are both 1.

After that, each subsequent number is derived by adding the two preceding numbers. So, the third number is 2, the sum of 1 and 1.

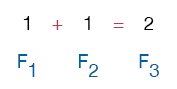
The fourth number is 3, the sum of 1 and 2.

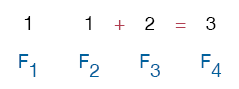
The fifth number is 5, the sum of 2 and 3.

The sixth number is 8, the sum of 3 and 5.

The seventh number is 13, the sum of 5 and 8, and so on.

To calculate a Fibonacci number, it would help to have a function that calculates Fibonacci numbers, just as we could just calculate the previous two and then add them.

Time travel

One way to think of this is using the idea of time travel: it is as if you think of being in two times at once.

---

In the present, we are writing a function, and want to use a helper function that works correctly. But this alone doesn't work because the helper function we want to use is the function we are writing. So we also think about being in the future after the function has been written and is correct.

This allows us to use the helper function now, knowing that it will be correct by the time we use it, since by then it will have been written.

Time travel for factorial

For the factorial example, we start writing the program in the present, naming the function fact, assuming that it will be correct in the future. Then we can use the function that we are writing in the function we are writing: define fact(num) return num * fact(num-1)

Here we return the number times the factorial of a number one smaller.

This type of function call is called a “recursive call”.

Tracing factorial

How does the function fact work? define fact(num) return num * fact(num-1)

Let's examine a trace to find out. To determine fact(4), we multiply 4 by fact(3): fact(4) ⇒ 4 * fact(3)

This in turn has the value of 3 multiplied by fact(2): 4 * fact(3) ⇒ 4 * 3 * fact(2)

Using the function again, fact(2) is replaced by 2 times fact(1): 4 * 3 * fact(2) ⇒ 4 * 3 * 2 * fact(1)

This is replaced by 1 times fact(0): 4 * 3 * 2 * fact(1) ⇒ 4 * 3 * 2 * 1 * fact(0)

This is now replaced by 0 times fact(-1): 4 * 3 * 2 * 1 * fact(0) ⇒ 4 * 3 * 2 * 1 * 0 * fact(-1)

This is replaced by -1 times fact(-2): 4 * 3 * 2 * 1 * 0 * fact(-1) ⇒ 4 * 3 * 2 * 1 * 0 * -1 * fact(-2)

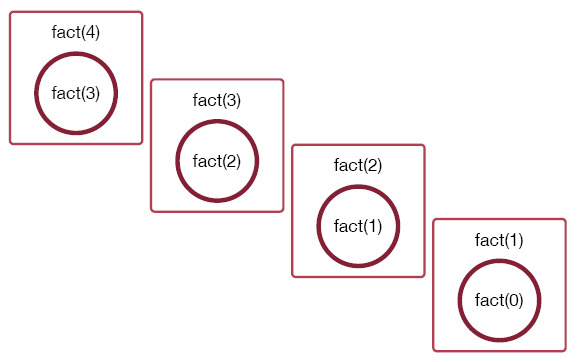
This process does not look very good since it does not stop. Multiplying by zero was bad enough, but having to continue forever is even worse. What happened?

Recursive calls without end

Visualization 1

Here's a way of visualizing the problem. Let's represent each function call using a rectangle and a function call from inside the fuction by a circle within this rectangle. Then, a call to fact(4) results in a call to fact(3):

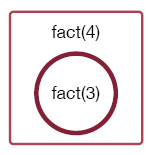
A call to fact(3) results in a call to fact(2):

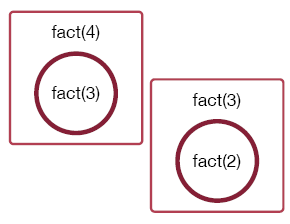
The call to fact(2) results in a call to fact(1):

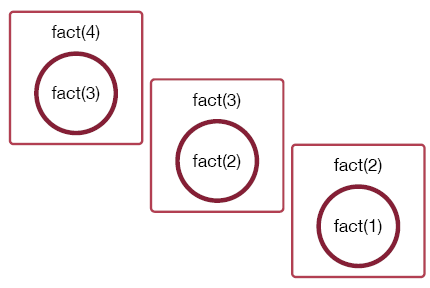
The call to which results in a never-ending sequences of function calls:

Visualization 2

Here's another visualization. Let's use circles for steps and a bigger circle for a function call. We represent each factorial function as consisting of two initial steps before the the function call and another two steps after the function call. Using circles, this is represented by two red circles, followed by a bigger red circle and two red circles. Don't worry about the exact number of steps - this is just to give you an idea of how the function calls work.

The steps in the first function call are executed until a function call is reached:

Then the steps in the second function call are executed until a function call is reached:

Then the steps in the third function call are executed until a function call is reached:

Then the steps in the fourth function call are executed until a function call is reached:

Then the steps in the fifth function call are executed until a function call is reached, and so on forever.

We will soon see how to solve this problem.

---