Storing elements in a sequence (Part 1)
Example: any number of pizza toppings

Images: foodandstyle/iStock/Thinkstock
Being able to use an index to find a character in a string made it easy to write while loops to process each character in order.
What if we wanted to process a sequence of numbers or strings or other data? Or what if we wanted group together an unknown number of related values such as, for example, pizza toppings, so that we could use the entire group as an input or output?
Sequences
Each language has at least one way to group data values and at least one way to put data values in an order. This does not mean that they are in increasing order for numbers or alphabetical order for strings, but rather any order you choose, like the order of characters in a string.
A sequence is a group of data values, given in order.
Other terms
Depending on the language, this is an array or a list.
Different languages support different types of sequences. Common names you might encounter are "array" and "list", which typically describe two different ways of grouping and ordering data. Just like in a string, the position of a value is its index and usually counting starts from zero:
An index is a position of a value. For example, as shown in the figure below, in the sequence [9, 2, 1, 4, 6, 5, 8, 3, 4, 1, 7], the index of 4 is 3.
9
0
2
1
1
2
4
3
6
4
5
5
8
6
3
7
4
8
1
9
7
10
Definition
Each value is an element or item of the sequence.
We refer to the individual values as elements or items.
String-like sequence functions
Not surprisingly, many functions that are useful for strings are also useful for sequences like extracting a single element or a subsequence. For example, considering the sequence [9, 2, 1, 4, 6, 5, 8, 3, 4, 1, 7], the same functions used to extract an element of a string can be used to extact the element 4. Also, the same function used to extract a substring can be used to extract the subsequence [4, 6, 5, 8].
9
0
2
1
1
2
4
3
6
4
5
5
8
6
3
7
4
8
1
9
7
10
Pseudocode for sequence functions and operations
We will use the same notation as we did for strings to determine the length of a sequence, finding a particular element, or concatenating two sequences:
- The pseudocode length([5, 2]) gives the result 2, which is the length of the sequence [5, 2].
- The pseudocode [5, 2, 7][0] gives the result 5, which is the the element with index 0 in the sequence [5, 2, 7].
- The pseudocode [5, 2, 7]+[4] gives the result [5, 2, 7, 4], which is the concatenation of the sequences [5, 2, 7] and [4].
Caution
Square brackets are used for both sequences and indices.
Notice that in the second example, square brackets are being used in two different ways. The brackets around 5, 2, and 7 indicate a list, and the brackets around [0] indicate an index. In the second example, the single number 4 inside brackets indicates a list of length 1, not an index.
Caution
The assumption that sequences can be concatenated may not hold for all languages.
Although we will use concatenation in our pseudocode, this may not be supported in all languages.
Sequences in memory
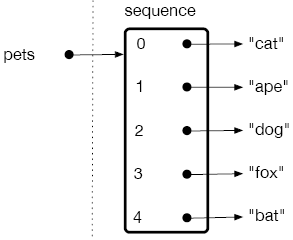
To visualize how a sequence is stored, you can imagine a variable name pointing to a group of indices and addresses, where each index points to the item stored in that location. For example, as shown in the figure below, consider the indices 0, 1, 2, 3, and 4 pointing to the items "cat", "ape", "dogs", "fox", and "bat" stored in some memory locations, respectively. As shown in the figure on the right, the variable "pets" points to the group of indices 0, 1, 2, 3, and 4.
"cats"
0
"ape"
1
"dogs"
2
"fox"
3
"bat"
4
Strings versus sequences
Given that sequences are more general and have a lot of the same functionality of strings, why not make a sequence of characters instead of a string?
Definition
Data is immutable if it cannot change.
Otherwise, it is mutable and can be changed using mutation.
The answer has to do with mutability. Data is either immutable, which means that it can't change, or mutable, which means that it can change. The process of change is called mutation. So far, all the data we have seen is immutable. Since strings are immutable, if you try to assign a new value to a position, an error results. For example, the pseudocode "cat"[1] ← "o" causes an error. But for a sequence, such an assignment can take place. For example, "pets"[4] ← "ant" is allowed.
Caution
Assigning a new value to an existing variable is not mutation. It changes the address associated with the name but not the data itself.
You might be wondering why numbers are immutable since we can change a variable to a different number. The key point is that mutation is not the same as assigning a new address in an address book.
Not mutation
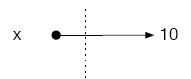
So our previous visualizations of memory did not represent mutation. We first assigned the value 10 to x: x ← 10.
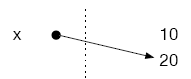
Next we assigned the value 20 to x: x ← 20. When we reassigned x to 20, we didn't change 10. Instead, we allocated new memory for 20 and then used that address in the address book entry for x. This is just like the example with the cranberries: we didn't mutate the apricots so that they turned into cranberries, we allocated new space for the cranberries and left the apricots alone.
 Language independent lessons
Language independent lessons