Iteration using for (Part 1)

Counted repetition

In many of the “while” loops we write, thescondition makes use of a counter. A “for” loop is a shorthand notation which includessboth the starting and ending values of the counter.

For example, consider a program consisting of two initial instructions, A and B, followed by a “for” loop with counter ranging from 1 to 4, loop body consisting of instructions C, D, E, and two instructions, F and G, after the loop. As usual, as shown in the figure, A, B, F, G are represented by red circles and C, D, E are represented by dashed blue circles.

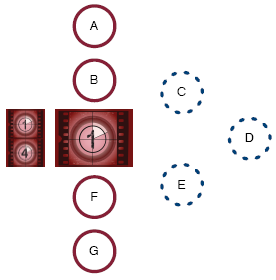
A B for counter from 1 to 4 C D E F G

---

In this example, the starting and ending values are 1 and 4. Like in the while loop, first the steps before the loop are executed, here A and B. In the first time through the loop, the counter has value 1 and all steps inside the loop body are executed. They are executed again when the counter has value 2, a third time when it has value 3, and a fourth time when it has value 4. Since the counter now matches the ending value,the last two steps, F and G, are executed. In summary, the order of steps executed are as follows: A B C D E C D E C D E C D E F G

Counted repetition — modified counter

Here is another example in which we've modified the counter to show that it does not need to start at the value 1. This program consisting of two initial instructions, A and B, followed by a “for” loop with counter ranging from 3 to 5, loop body consisting of instructions C, D, E, and two instructions, F and G, after the loop. As usual, as shown in the figure, A, B, F, G are represented by red circles and C, D, E are represented by dashed blue circles.

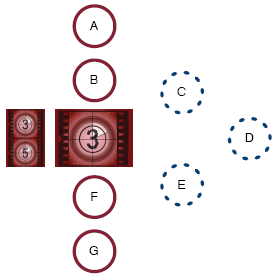
A B for counter from 3 to 5 C D E F G

---

Again, we start with the steps outside the loop. The first time through the counter starts at the starting value, that is, 3, and the steps C, D, and E are executed. Next the counter has value 4 and finally value 5. Since we have reached the ending value, we now execute steps F and G. In summary, the order of steps executed are as follows: A B C D E C D E C D E F G

Comparing while and for loops

For both “while” and “for” loops, we start bys expressing the task as iteration. After that, the next and last step to forming a “for” loop is to specify starting and ending values. That is, we don't need to write a condition, set initial value of variables, or make sure the condition can change. Since a “for” loop is so much easier to use, why not always use a “for” loop?

As we'll see, sometimes using “while” is our only option, and sometimes we have a choice, but still choose the “while” loop for clarity.

Revisiting repeated greetings

To see the difference between the types of loops, let's revisit the function that consumes a saying and a number of repetitions and uses iteration to repeatedly print the variable saying: define greeting(saying, repetitions) while repetitions > 0 print(saying) repetitions ← repetitions - 1

Here is the function written using a "for" loop: define greeting(saying, repetitions) for counter from 1 to repetitions print(saying)

We don't need to update repetitions in the loop, as that is handled for us automatically.

Example: triangular numbers

We can use iteration to determine a triangle number, that is, a number of dots that form a triangle.

---

---

Three dots are needed to form a triangle with 2 dots on each side, six dots to form the third triangular number, ten dots to form the fourth triangular number, fifteen dots to form the fifth triangular number, and so on. How can we use iteration to find a triangular number? We take the sum of 1, 2, 3, 4, and 5 for the fifth triangular number.

Writing the function

define triangle(num) total ← 0 for counter from 1 to num total ← total + counter return total

To write this as a function that consumes which triangular number to create, we iteratively add in larger and larger numbers. That is, we use a counter with values from 1 up to num, at each iteration adding the current value of counter to the total, and returning the final value of total. We don't have worry about initial values of variables used in the condition, since there is no condition. However, we still need to initialize any variable updated in the loop, in this case, total. Zero is a good initial value, as all the number scan be added in one by one.

Example: factorial

Another special type of number is a factorial, where the factorial of a number is the product of all integers from 1 up to the number itself:

The factorial of n is the product 1 * 2 * ··· * (n-1) * n

For example, the factorial of 5 is 1 * 2 * 3 * 4 * 5 = 120.

Expressed as iteration, we want to loop over all numbers from 1 to num, multiplying them into our total. This suggests that our starting and ending value are 1 and num. define fact(num) total ← 1 for counter from 1 to num total ← total * counter return total

In the body of the loop, we multiply in the counter to the total, and total is the value that we return. In this case, we set total to the value 1. Why not 0? Zero is a fine choice when we're adding values to a starting value. If we started with zero here, we'd keep getting zero, no matter how many numbers we multiplied in.

---