Recursion (Part 3)

Time travel for Fibonacci numbers

Let's use the recursion recipe to write a recursive function for Fibonacci numbers.

---

define fact(num) return num * fact(num-1)

In the present, we start writing our function. We travel to the future in which the function is correct.

Writing the function

A Fibonacci number is the sum of the two previous Fibonacci numbers. We know how to use recursion here: the two smaller Fibonacci numbers are both closer to the base case.

We know that the base cases are the first and second Fibonacci numbers, each with value 1. Base cases occur when num has value 1 or 2. define fib(num) if num <= 2 return 1 else return fib(num - 1) + fib(num - 2)

For the recursive case, we have two recursive calls, one to num minus one and one to num minus two. Finally, we verify that for any value of num greater than 2, the function will return values for num minus one and num minus two, as needed for the recursive case to work.

Wasted time

You may have noticed that this function may not be the most efficient way to solve the problem. Again, let's represent a function call by a square and recursive function call within this function by circles. Then, fib(5) is represented by a square with two circles inside to represent the recursive function calls fib(4) and fib(3) within fib(5).

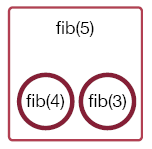
The first is to call fib(4).

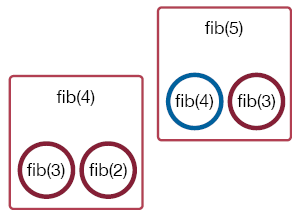
The call to fib(4) in turn calls fib(3).

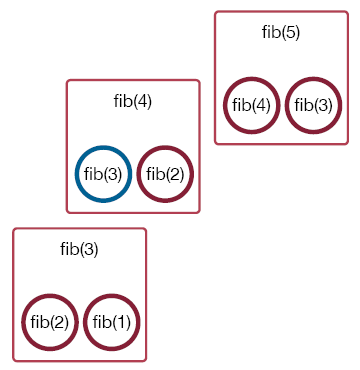
The call to fib(3) in turn calls fib(2).

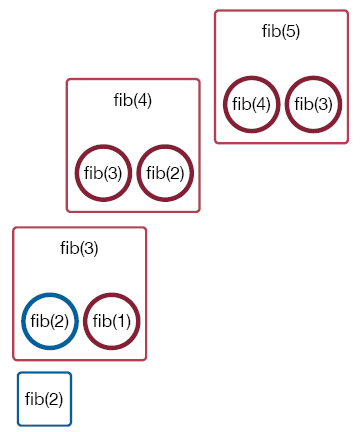
Since that is a base case, the value is returned. This allows fib(1) to be called.

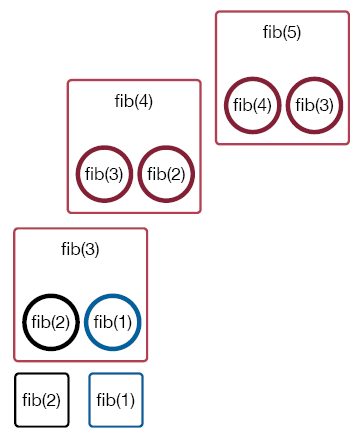
This is also a base case, so now the call to fib(3) can be completed. Since the call to fib(4) is no longer waiting for the call to fib(3), the next function call is possible, namely a call to fib(2).

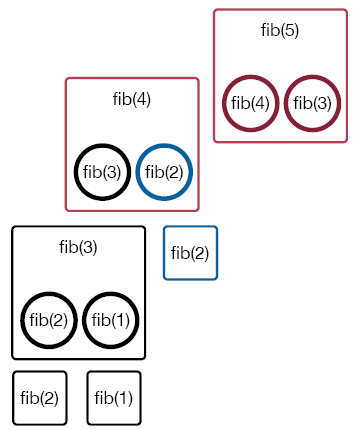
Since that is a base case, the call to fib(4) can be completed, returning a value to the call to fib(5), which then calls fib(3).

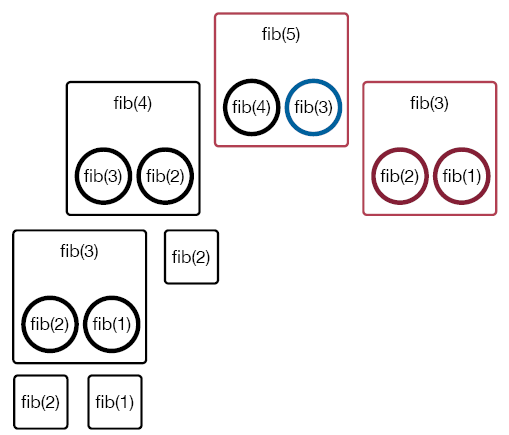
fib(3) calls fib(2). Since this is a base case, this can be completed.

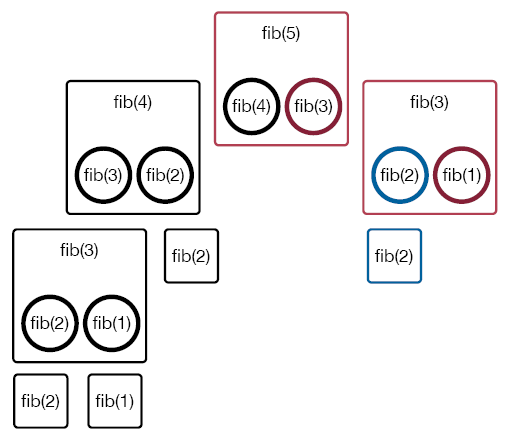
Next, fib(1) is called. Since fib(1) is a base case, it can be completed and return a value to fib(3). Now, fib(3) can be completed and returns a value to fib(5). This completes fib(5).

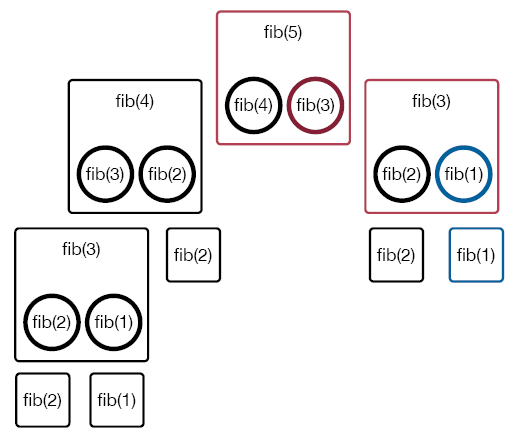
This is correct but notice that we called fib(3) twice. Is that a problem? Let's look a little closer.

Calls to fib(3)

• fib(5) calls fib(3) 2 times
• fib(7) calls fib(5) 2 times, and fib(3) 4 times
• fib(9) calls fib(7) 2 times, fib(5) 4 times, and fib(3) 8 times
• fib(11) calls fib(9) 2 times, fib(7) 4 times, fib(5) 8 times, and fib(3) 16 times

If we had started with a call to fib(7) instead of fib(5), it would have called fib(5) twice, and each of those calls would have called fib(3) twice, for a total of 4 calls of fib(3). That looks like adding two each time, but it is worse than that: a call to fib(9) would result in 8 calls of fib(3), namely a doubling of the number of calls. A call to fib(11) would result in 16 calls of fib(3), and so on.

Saving resources

There are ways of making recursion better so that we don't waste so much time and space. In fact, there are ways of making programs better in general. We haven't talked about them in this course.

Recursion on strings or sequences

Functions for all strings or sequences (length n)

• Base case: empty (n = 0)
• Recursive case: concatenate length 1 + length n-1 (n > 0)

Suppose we wanted to use the ideas of recursion on strings or sequences instead of numbers. You can think of a string as being formed from two smaller strings, namely a string of length one and a string of length one less than the length of the original string. That is, unless the original string is the empty string. So our base case, which can't be handled by the recursive case, is the empty string, and the recursive case uses an input that is closer to being empty, that is, closer to the base case. The same idea holds for sequences.

Functions for nonempty strings or sequences (length n)

• Base case: length 1 (n = 1)
• Recursive case: length 1 + nonempty of length n-1 (n > 1)

If we are only considering non-empty strings or sequences, then we can think of one being formed from two smaller strings or sequences, namely a string or sequence of length one and a non-empty string or sequence of length one less than the length of the original string or sequence, except for a non-empty string or sequence of length 1, which is a base case. Again, the recursive case applies to an input closer to the base case.

The amount of time required may depend on how the smaller and larger strings or sequences are formed.

Example: finding the maximum element

Suppose we wished to find the maximum element in a non-empty sequence of numbers. For example, consider the sequence [3, 6, 5, 2, 7, 4, 10, 1].

We can accomplish this by using our function on smaller sequences. For example, the smaller sequences [3, 6, 5, 2] and [7, 4, 10, 1].

Similarly, we again apply our function on smaller sequences still. For example, the smaller sequences [3, 6], [5, 2], [7, 4], and [10, 1].

Depending on the language, this might be slow due to the time and space needed to create new sequences at each step.

Using first and last markers

Another approach would be to keep the same sequence, but instead to mark the indices of the subsequence to be considered.

In this example, we could focus on the first half of the sequence by setting last to 3.

On the first quarter, we set last to 1.

For other pieces, we would also change first to values other than 0.

Using a wrapper function

• Write a recursive generalized version of the function for any first and last positions.
• Write a nonrecursive wrapper function to set initial values of first and last.

We write a function that has three inputs: the sequence, the first index, and the last index. This is even more general than the function we originally wanted to write, since we can now choose any arbitrary subsequence. define seq_max_part(seq, first, last)

To have a function that looks at all items in a sequence, we write another very simple function which does one thing: it calls our generalized function with the first and last positions set to the first and last positions in the sequence and returns the value. define seq_max(seq) return (seq_max_part(seq, 0, length(seq)-1))

Writing the generalized version of the function

To write the generalized function, we first figure out how to use recursion. To use the same function on an input closer to the base case, we figure out the maximum of the first element and the result of using the function on the rest of the sequence. For the base case, there is only a single element in the range from first to last and that is then the maximum. So, base cases first and last are equal. Otherwise, i.e., for the recursive case, we return the maximum of the first value in the range and the result of using our function on the rest of the range. All possibilities are covered as long as first is less than last, which is guaranteed by the fact that we use the wrapper function only on non-empty lists. define seq_max_part(seq, first, last) if first == last return seq[first] else return max(seq[first], seq_max_part(seq, first + 1, last))

Putting it all together

Putting it all together, we get the following pseudocode. define seq_max(seq) return(seq_max_part(seq, 0, length(seq)-1)) define seq_max_part(seq, first, last) if first == last return seq[first] else return max(seq[first], seq_max_part(seq, first + 1, last))

---