Recursion in Python (Part 1)

Example: summing a list of numbers

There is no special syntax for recursion in Python that sets it apart from other languages, though there are some handy uses of syntax we've already seen. As a first example, suppose we wish to sum a list of numbers. How can we express this problem in terms of a problem on an input closer to the base case?

## seq[0] + sum(seq[1:])

A non-empty list of numbers can be viewed as the concatenation of the first number and a smaller list of numbers. So if we have a function that sums the smaller list of numbers, all we need to do is add in the first number.

---

def sum(seq):

Here in the present, we'll write the function sum, assuming that it will be correct in the future. Notice that the slice function gives us a very nice way of extracting the smaller list.

---

    if len(seq) == 0:
        return 0

We first make sure that we have a base case. An empty list is not defined as the concatenation of a number and a smaller list, and hence is not covered by the recursive case. So all we need to do is figure out what the sum of zero numbers is.

---

    else:
        return seq[0] + sum(seq[1:])

For the recursive case, we return the value we determined earlier, making use of a call to the function we are writing.

---

def test_sum():
    example = [1, 2, 3, 4]
    assert sum(example) == 10
    assert sum([4]) == 4
    assert sum([]) == 0

test_sum()

We now test our code, making sure that we cover both empty and non-empty cases.

---

Here's our code when all parts are put together:

## seq[0] + sum(seq[1:])

def sum(seq):
    if len(seq) == 0:
        return 0
    else:
        return seq[0] + sum(seq[1:])

def test_sum():
    example = [1, 2, 3, 4]
    assert sum(example) == 10
    assert sum([4]) == 4
    assert sum([]) == 0

test_sum()

Slices are a good learning tool for understanding recursion.

Although in this course we're not concerned with efficiency, in the future you will learn other approaches that are more efficient.

---

Example: finding the maximum element

We've already looked at the problem of finding the maximum element in the list using indices to narrow down the search. In this case, we'll use slices again. How do we express the maximum in a list in terms of the maximum in a smaller list?

## max(seq[0], seq_max(seq[1:]))

Using the slice function again, we simply compute the maximum of the first element and the largest element in the rest of the list.

---

def seq_max(seq):

We now write the helper function that we'd like to use.

---

    if len(seq) == 1:
        return seq[0]

For the base case, we have a list of length 1, as it doesn't make sense to talk about the maximum element in an empty list. The value in this case will be the single item in the list.

---

    else:
        return max(seq[0], seq_max(seq[1:]))

Our recursive case is handled using the expression we developed earlier. Again, we assume that the function works correctly.

---

def test_seq_max():
    unsorted = [4, 7, 2, 4, 1, 3, 2, 8, 7]
    assert seq_max(unsorted) == 8
    assert seq_max([4]) == 4

test_seq_max()

Finally, we test our function, again making sure to have both a base case, that is a list of length one, and a general case, that is a list of length greater than one.

---

Here's our code when all parts are put together:

## max(seq[0], seq_max(seq[1:]))

def seq_max(seq):
    if len(seq) == 1:
        return seq[0]
    else:
        return max(seq[0], seq_max(seq[1:]))

def test_seq_max():
    unsorted = [4, 7, 2, 4, 1, 3, 2, 8, 7]
    assert seq_max(unsorted) == 8
    assert seq_max([4]) == 4

test_seq_max()

Be extra careful when a base case is non-empty, as the result usually requires a little more thinking than for an empty base case.

---

Example: palindromes

As our third example, consider again the problem of palindromes. If the first and last character match, then the entire string is a palindrome if and only if the remaining substring is a palindrome.

---

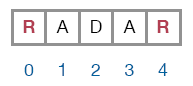
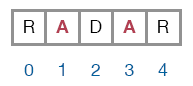
For example, the string “RADAR”, is a palindrome if the substring “ADA” is a palindrome since the first character, “R”, and the last character, ”R”, match. So, if you want to check for a palindrome, the most desirable helper function is a function that checks for a palindrome.

---

Writing the function

## entry[0] == entry[-1] and is_pal(entry[1:-1])

To express the result in terms of the substring, we check that the first and last characters are the same and then use the helper function on everything else.

---

def is_pal(entry):

In the present, we write the function that we want to use.

---

    if len(entry) <= 1:
        return True

What is left when we can no longer remove the first and last characters? Depending on whether the length of the original string was even or odd, there will either be a single character or an empty string. In both cases, the answer is True.

---

    else:
        return entry[0] == entry[-1] and \
                           is_pal(entry[1:-1])

Otherwise, we fill in the recursive case using the expression we formed.

---

def test_is_pal():
    """Tests correctness of is_pal
    """
    assert is_pal("") == True
    assert is_pal("a") == True
    assert is_pal("otto") == True  
    assert is_pal("bob") == True
    assert is_pal("apple") == False
    assert is_pal("area") == False

test_is_pal()

Finally we test our function.

---

Here's our function when all parts are put together:

## entry[0] == entry[-1] and is_pal(entry[1:-1])

def is_pal(entry):
    if len(entry) <= 1:
        return True
    else:
        return entry[0] == entry[-1] and \
                           is_pal(entry[1:-1])

def test_is_pal():
    """Tests correctness of is_pal
    """
    assert is_pal("") == True
    assert is_pal("a") == True
    assert is_pal("otto") == True  
    assert is_pal("bob") == True
    assert is_pal("apple") == False
    assert is_pal("area") == False

test_is_pal()

---