Built-in functions in Python (Part 2)

User input

Like most languages, Python has some functions that allow interaction with the user. The function input is used to prompt the user to enter a value. The input to the function input is a string that is printed to the screen. Notice that string is entered by using quotes around it - we will learn more about strings later. Also, notice that I added a space after the colon so that the user's input would be more readable. The following code

print(input("Enter a string: "))

gives the output containing an input box next to the string “Enter a string: ”:

Enter a string: 

The output to the function input is whatever the user types in. For example, typing in “cat” in the input box and hitting enter gives the output

 
Enter a string: cat

Since I typed in “cat”, the result of printing the result of the function call is printing the string “cat”. Adding a prompt to the user isn't necessary, as long as the user knows what to do without being told. For example, the code print(input()) gives the output with no text:

Again, whatever the user enters is printed. For example, entering “cat” in the input box and hitting enter gives the output

cat

What if we instead ask for a number? For example, consider the code

print(2 * input("Enter a number: "))

We're asking the computer to multiply by two whatever is entered. This gives the output

Enter a number: 

Entering the number 5 and hitting enter gives “55” as the output:

Enter a number: 55

What happened? That's not the multiplication I learned! What happened is that even if we ask for a number, the computer always interprets what is typed as a string. This is a good example of needing to know the data types of inputs and outputs. We'll learn later why what was printed was two copies of the string “5”.

---

To get a number, we can use the built-in function “int” that consumes a string and produces an integer. For example, consider the code

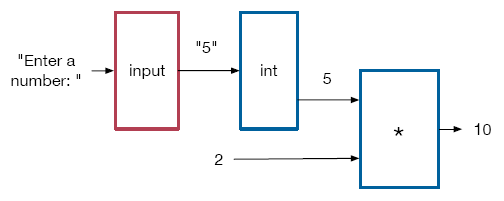
print(2 * int(input("Enter a number: ")))

Here we are asking to convert the input string to an integer and then multiply it by 2. This produces an output with an input box. Entering the number 5 and entering gives 10, which is the correct answer:

10

Notice the order of operations in the function composition: the output of input, which is a string, is the input to int. The output of int is an integer, which we can multiply by 2.

---

Here is a summary of what we learnt.

• Use input() to prompt the user for input.
• The prompt string can be omitted.
• What the user types is the output of the function call.
• What the user types is interpreted as a string.

To prompt a user for input, use input, with an optional string in the parentheses. You can then use what the user types as the output of the function call - but remember, it will be interpreted as a string.

---

Functions that check and change types

You can avoid a lot of trouble by being sure to know the types of data that are consumed and produced by a function that you are using. But what if you don't know what type of data you have? The type function determines the type of values or expressions. The following code

print(type(5))
print(type(5.0))
print(type("string"))

gives the output

<class 'int'>
<class 'float'>
<class 'str'>

But what if you don't like the answer you get? We already saw the int function. It can be used to make any number into an integer. The following code

print(int(5))
print(int(5.1))
print(int(5.9))
print(int(-5.1))
print(int(-5.9))

gives the output

5
5
5
-5
-5

Notice that the way that this is achieved for floating point numbers is by truncating any numbers that follow the decimal point. But that's not all: int can also be used to make a string into an integer. For example, print(int("5")) gives the output 5. The string has to be the string representation of an integer, like the number 5 in this example. If we try to use the function on the string dog, we get an error message: the code print(int("dog")) gives the output

Traceback (most recent call last):
  File "<string>", line 1, in <module>
ValueError: invalid literal for int() with base 10: 'dog'

Don't worry if you don't understand all the words here. The fact that it is a value error tells you that there is a problem with the value, which is incentive to change it. Keep in mind that using int on strings only words for strings of digits, not for a word representation of an integer. The code print(int("five")) again gives an error message:

Traceback (most recent call last):
  File "<string>", line 1, in <module>
ValueError: invalid literal for int() with base 10: 'five'

If the input string represents a floating point number, again the error message complains about the value. For example, the code print(int("4.3")) gives the error message

Traceback (most recent call last):
  File "<string>", line 1, in <module>
ValueError: invalid literal for int() with base 10: '4.3'

So be careful how you use int on strings. There are also functions that make numbers or strings into floating point numbers or strings. The following code

print(float(5), float(5.0), float("5.0"), float("5"))
print(str(5), str(5.0), str("5.0"), str("5"))

gives the output

5.0 5.0 5.0 5.0
5 5.0 5.0 5

Notice in the last example of float that even if the string is a string form of an integer, the function still works, by making the integer into a floating point number. Also notice the use of commas to join values that we wish to print.

---

Functions that check and change types

The functions we used are summarized here along with what we learned about printing multiple values on one line.

Function	Python
determine type	type(5)
make into integer	int(5)
make into floating point	float(5)
make into string	str(5)

---

Entering and displaying numbers

Even when you know the type of data, the ways floating point numbers are displayed might surprise you.

In particular, when numbers are very big or very small, Python uses a notation that represents the number as a not-so-big and not-so-small number multiplied by a power of 10. In translating from the notation to Python, a letter e is used, with a plus for a positive power and a dash to indicate negation for a negative power. The table below gives two examples:

Scientific notation	Python
2.435 × 1095	2.435e+95
2.435 × 10-95	2.435e-95

Don't worry, you are not going to be expected to master scientific notation.

Such numbers will not be used in this course. That said, you might run into scientific notation when experimenting with Python, so it is worth your understanding a little bit about it.

---

Encountering scientific notation in Python

We've already seen how approximate values are stored for floating point numbers. For example, the following code

print(100000000000000000000000000000009)
print(100000000000000000000000000000009.0)

gives the output

100000000000000000000000000000009
1e+32

In the first number there is no decimal point, so it is stored as an integer. But by putting a decimal point in the second number, we've allowed the computer to store it as an approximation. It not only appears in scientific notation, but the digit 9 has been lost. You might think that you could get around the problem of numbers looking different upon entry and upon display, but that isn't even true for all numbers entered using scientific notation. For example, the following code

print(2e+20)
print(2e-20)
print(2e+5)
print(2e-3)

gives the output

2e+20
2e-20
200000.0
0.002

If we make the number big enough or small enough, it gets stored as infinity or zero. For example, the following code

print(2e+900)
print(2e-900)

gives the output

inf
0.0

For a very large number, not all the digits will be stored. For example, the code

print(123456789123456789123456789.0)

gives the output

1.2345678912345679e+26

But why are the last two digits 7 and 9 instead of 7 and 8? What happened is when the computer chose when to “chop off” the last digits, it rounded up. In this particular instance, it rounded up the number to 17 significant figures: 123456789123456789123456789.0 is rounded up to 123456789123456790000000000.0, where the latter number contains only 17 significant digits. Then scientific notation was used to represent the rounded off number, i.e., 1.2345678912345679 × ²⁶. All of this explanation is not designed to worry you but to reassure you - first, that we won't be using such numbers, and second, if you do encounter them in your experimentation, you'll understand what is going on.

---