Creating functions in Python (Part 4)

Global and local reuse

We continue our discussion of the reuse of names by considering what happens if we use a name in both a permanent address book and a temporary address book.

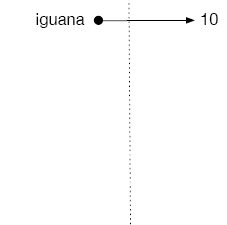
iguana = 10

def big(num):
    iguana = num + 3
    return iguana

---

We enter iguana in the permanent address book as a variable with value 10 and enter big in the permanent address book as the name of a function.

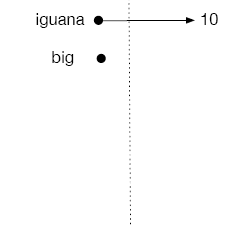
iguana = 10

def big(num):
    iguana = num + 3
    return iguana

print(iguana)

---

When we ask the computer to print "iguana", print(iguana), the function big is not used, and hence no temporary address book is created. The value printed will be 10.

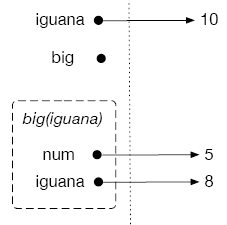
iguana = 10

def big(num):
    iguana = num + 3
    return iguana

print(iguana)
print(big(5))

---

If we call big(5), a temporary address book is created, with parameter num having value 5 and variable iguana having value num + 3, or 8. The value printed will be 8.

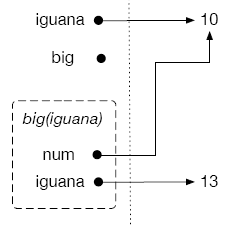
iguana = 10

def big(num):
    iguana = num + 3
    return iguana

print(iguana)
print(big(5))
print(big(iguana))

---

If we call big(iguana), a temporary address book is created, with parameter name num being assigned to the value stored with the name iguana in the permanent address book, and now the temporary address book will create a local variable iguana with value num + 3, or 13. This is the value that will be printed.

Consider the example code

def jackal(num):
    return num

def large(age):
    jackal = age + 3
    return jackal

print(jackal(10))
print(large(10))

which gives the output

10
13

In this example, jackal is the name of a function and also the name of a local variable in another function. When we call jackal(10), we are using the permanent address book to find the name of the function. This results in the value 10 being printed. If we call the function large(10), then in the temporary address book, the parameter age has value 10, and the local variable jackal has value 10 + 3, or 13. This results in the value 13 being printed. What if we call large(jackal)? Running the code

def jackal(num):
    return num

def large(age):
    jackal = age + 3
    return jackal

print(jackal(10))
print(large(10))
print(large(jackal))

gives the output

10
13
Traceback (most recent call last):
  File "<string>", line 10, in <module>
  File "<string>", line 5, in large
TypeError: unsupported operand type(s) for +: 'function' and 'int'

What we are trying to do is to use the function jackal as input to the function large. The error message “unsupported operand type for + ” indicates that we ran into trouble when trying to add age, which is the function jackal, to the number 3. The error was a consequence of what we were trying to do, namely add a function and a number, not the use of the name both globally and locally.

To conclude, we can use the same name in both permanent and temporary address books, though we should keep in mind that just because we can do something doesn't mean we should do it. If it is clearer to use different names, use different names.

---

Example: gold cost for a ring

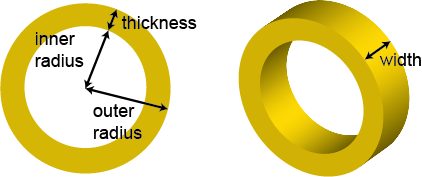
With all this in mind, let's create a function that determines the cost of a gold ring using the

• circumference of the finger,
• thickness of the ring,
• width of the ring, and
• cost of gold per cubic mm.

We'll use a constant for the cost of a cubic millimeter of gold and use as parameters the finger circumference, width of the ring, and thickness of the ring. We can think of the ring as a cylinder with smaller cylinder removed. So most of our work is in finding the volume of the two cylinders. We know how to compute the volume of a cylinder given the area of the circle at one end and the length. Since the length here is the width of the ring, our tasks are as follows:

• Determine the inner radius.
• Determine the outer radius.
• Determine the volumes.
• Compute the total volume from the two volumes.
• Calculate the cost of the ring.

---

Following the recipe

Assuming that the cost of gold is $0.8098 per cubic mm.

import math

COST_MM3 = .8098 # cost per cubic mm

Since we're likely to use π, we'll start by importing the math module and defining our constant.

---

def area_circle(radius):
    return math.pi * radius ** 2

def volume_cylinder(radius, length):
    return length * area_circle(radius)

We'll define some helper functions to help compute the volume of the cylinder. I've chosen to use the radius as a parameter for both functions to illustrate that the same name can be used for both.

---

def circ_to_radius(circ)

Since determining radius from circumference is a task that might be useful in other programs, we create a helper function. To create the header of the helper function, we need a name for the function and a name for the parameter. I am reusing the name circ which is also the name of a parameter for ring_cost.

---

    return circ / (2 * math.pi)

Since the circumference of a circle is 2 × π × the radius, to get the radius we divide the circumference by (2 × π).

---

def ring_cost(circ, width, thickness):

We add the function header. Let's call the function ring_cost and our three parameters circ for circumference, width, and thickness. We don't have the inner radius, just the circumference.

---

    ## Determine inner radius
    radius = circ_to_radius(circ)

We now complete the first task. Notice that I'm reusing the name radius, which already appears as a parameter name in both area_circle and volume_cylinder. When we call ring_cost, the input for finger circumference will have the local name circ. When circ_to_radius is called, the value will then also be assigned to the local name circ in that function call, with no interference.

    ## Determine outer radius
    outer_radius = radius + thickness

The outer radius of the circle is the radius of the finger plus the thickness of the ring.

---

    ## Determine volumes
    inner_volume = volume_cylinder(radius, width)
    outer_volume = volume_cylinder(outer_radius, width)

We can now use our helper function to determine the volumes of the cylinders. Notice that radius is both a local variable in ring_cost and the parameter in volume_cylinder. Again, there will be no interference.

---

    ## Compute total volume
    total_volume = outer_volume - inner_volume
    ## Calculate cost
    return total_volume * COST_MM3

Computing the total volume is easy, as is calcuating the total cost.

---

print(ring_cost(57, 2, 2))
print(ring_cost(10, 5, 3))

Finally, we can verify that the function works correctly.

---

Putting them all together

Here is the complete program when all parts are put together:

import math

COST_MM3 = .8098 # cost per cubic mm

def area_circle(radius):
    return math.pi * radius ** 2

def volume_cylinder(radius, length):
    return length * area_circle(radius)

def circ_to_radius(circ):
    return circ / (2 * math.pi)

def ring_cost(circ, width, thickness):
    ## Determine inner radius
    radius = circ_to_radius(circ)

    ## Determine outer radius
    outer_radius = radius + thickness

    ## Determine volumes
    inner_volume = volume_cylinder(radius, width)
    outer_volume = volume_cylinder(outer_radius, width)
 
    ## Compute total volume
    total_volume = outer_volume - inner_volume

    ## Calculate cost
    return total_volume * COST_MM3

print(ring_cost(57, 2, 2))
print(ring_cost(10, 5, 3))

---

Running the program gives the output

204.98689384701612
235.95277788946566

This confirms that our program works correctly.

---