Booleans (Part 1)

Handling different situations

In writing programs, often we want to be able to ask a question in order to determine which course of action to take. In many real-life situations, there are different calculations to be made depending on the age of the customer, cost of a purchase, or other information.

To determine whether to give the discount for seniors, we might ask if the customer is at least 65 years old. If the answer is "yes", we apply a senior discount. If the answer is "no", we don't.

---

To determine whether an order is eligible for free shipping, we might ask whether the total cost of the order is at least some threshold, say $100. Again, our course of action will depend on the answer: free shipping if the answer is yes, or applying a shipping charge if the answer is no.

---

Representing yes and no

How might we represent the answers to the questions? We could use the strings "yes" and "no", though we would have to remember whether we are using lower case or upper case. We could use other strings with the same meaning. For example, "Most definitely" and "Are you kidding?". We could even use arbitrary strings, like "octopus" and "panda". We could use the number 1 for yes and the number 0 for no, again having to remember which number means what and whether you used integers or floating point numbers. We can use any other two numbers like 3 and 12. How can we decide amongst so many choices?

Throughout the course, we'll use a simple principle about keeping things simple.

Why make things more complicated than necessary? We will later appreciate this choice, as it will both help to avoid errors and help to find any that do occur.

---

Booleans

A Boolean has two possible values: True or False.

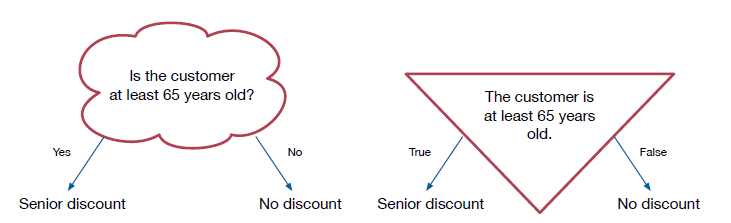
So in keeping with the principle, we're going to use a very simple data type called a Boolean. It is so simple that there are only two values, true and false. That means that if we have a yes/no question, like the one about the age of the customer, we can change it into a statement that is either true or false. The answer to the question is yes exactly when the statement is true. That is, answering yes to "Is the customer at least 65 years old?" is the same as saying that the statement "The customer is at least 65 years old" is true.

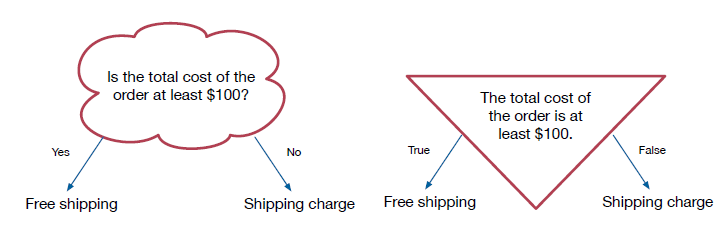
We can make the same transformation for the other question we asked. Here we change "Is the total cost of the order at least $100?" into the statement, "The total cost of the order is at least $100". " Again, the answer to the question being yes is equivalent to the statement being true.

Just like a mathematical expression can be evaluated to determine a numerical value, a Boolean expression can be evaluated to determine a Boolean value.

The term condition is used when a Boolean expression is used to make a choice, like we are doing here. We'll use both of these terms.

---

Built-in operations and functions using Booleans

To create Boolean expressions, we need functions. As you've probably already guessed, there are built-in functions that consume and produce Booleans. One of the simplest functions, not, returns "False" when the input has the value "True", and it returns "True" when the input has the value "False". The input can be any Boolean expression. Most languages have built-in functions that allow you to check if a value is an integer, for example, or various properties of numbers. These types of functions return Booleans. Here is a summary of what we just discussed:

• The pseudocode not True returns the value False.
• The pseudocode not False returns the value True.
• The pseudocode is_integer(5) returns the value True.

There are also built-in functions that allow you to check how two values are related to each other. An operation that compares two values is called, not surprisingly, a comparison.

You are using a comparison when you ask if 5 is less than 8 or if negative one is greater than or equal to 12.

Some common comparisons include <,>,<=,>=, and ==. Here are some examples of their usage:

• The pseudocode 5 < 8 gives the value True.
• The pseudocode -1 >= 12 gives the value False.
• The pseudocode 4 == 4 gives the value True.

Notice that in our pseudocode, this is written with the "greater than" before the "equal" - saying it helps with remembering the order of symbols. For our pseudocode, I am using two equal signs to denote equality, since this is common in languages that use a single equal sign for assignment. Comparisons are not limited to numbers. Checking for equality is important for just about every type of data, and when there is an order to values, such as alpabetical order for strings, there are also comparisons for checking the order of values.

---

Boolean expressions

Some examples of Boolean expressions are not 5 < 8 and "cat" <= "dog".

Just like we can put together numbers and operations or functions into a larger expression, we can form a Boolean expression that evaluates to either true or false. We will soon put these to use in creating programs.

---