Booleans (Part 2)

Asking more complex questions

What if we want to ask a question that cannot be expressed using a single comparison, such as asking whether or not x is the range from 10 to 20? As before, we can translate the question into a statement.

Translation of the question "Is x in the range from 10 to 20?" to the statement " x is in the range from 10 to 20".

Looking more closely, we can express our statement using two Boolean expressions, namely, that x is greater than or equal to 10 and that x is less than or equal to 20. Moreover, we want both of the expressions to be true.

Using and on expressions

We use "and" to join together smaller Boolean expressions to form a more complex Boolean expression. I'm going to assume that each of the larger expressions will be used to make a decision, so I'll call the larger ones "conditions" and the smaller ones "smaller expressions": (10 <= x) and (x <= 2) is the condition and the smaller expressions are 10 <= x and x <= 20. Let us use the labels A and B to refer to the smaller expressions 10 <= x and x <= 20, repectively. The condition is True exactly when both smaller expressions are True.

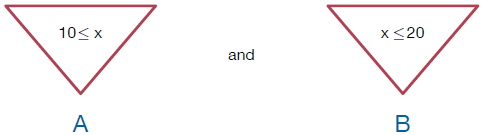
Using and on three or more smaller expressions

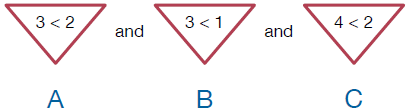
We can use the same idea when we have "and"s joining a sequence of smaller expressions. A condition using and is True when all smaller expressions are True. Consider an example where the labels A, B, and C refer to the smaller expressions are 3 < 2, 3 < 1, and 4 < 2. Then the condition will be true when all three of the smaller expressions A, B, and C are true.

Examples using and

Let's look at a few more examples. Is 3 < 2 and 3 < 1 and 4 < 2 true? No, since all of the smaller expressions are false.

The condition (3<2 and 3<1 and 4<2) is false since all smaller expressions are false.

Is 3 < 2 and 3 < 1 and 2 < 4 true? Here the last smaller expression is true, but that still isn't good enough; again, the condition is false.

The condition (3<2 and 3<1 and 2<4) is false since at least one smaller expressions are false.

What about 2 < 3 and 3 < 1 and 2 < 4 ? Still no good since the middle smaller expression is false.

The condition (2<3 and 3<1 and 2<4) is false since the middle smaller expression is false.

How about 2 < 3 and 1 < 3 and 2 < 4 ? Finally, we have three true smaller expressions joined by "and"s, which makes the condition true.

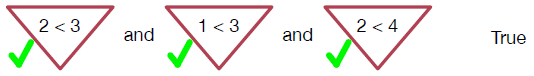
The condition (2<3 and 1<3 and 2<4) is true since all three smaller expressions are true.

Choice of conditions

What if there is a situation when you allow a choice of options, such as allowing a discount for two different age ranges? For example, allowing discounts for people younger than 21 or at least 65.

Again, we can express the condition using two smaller expressions: n < 21 and 65 ≤ n. This time, we don't need for both smaller expressions to be true. Which is good since a number can't be both less than 21 and greater than or equal to 65. In general, we can use "or" to join any smaller expressions. We want the condition to be true when at least one of the smaller expressions is true. A condition using or is True when at least one smaller expression is True.

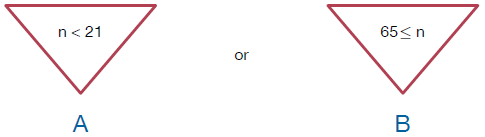
The condition (n<21 or 65<=n) is true when at least one of the two smaller expressions are true.

Even though from the use in English, we use "or" to mean "one or the other but not both", here "or" means "one or the other or both".

Caution

We use “or” to mean “one or the other or both”.

Using or on expressions

We can generalize from our condition, which is made up of two smaller expressions, to a condition of the form A or B or C, which is true when at least one smaller expression is true. Again, remember that a condition using or is True if at least one smaller expressions is True.

Condition of the form (A or B or C): (2<3 or 3<1 or 2<4).

Examples using or

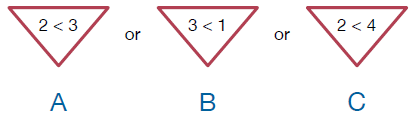
Here are some more examples to consider. In this first example, the condition is 2 < 3 or 3 < 1 or 2 < 4. The first and last smaller expressions are true, so the condition is true.

The condition (2<3 or 3<1 or 2<4) is true since since the first and the last smaller expressions are true.

Now consider 2 < 3 or 1 < 3 or 2 < 4. Here all three are true, which means that at least one is true, again resulting in true.

The condition (2<3 or 3<1 or 2<4) is true since since all smaller expressions are true.

In the condition 3 < 2 or 1 < 3 or 4 < 2, the middle expression is true here, which is good enough for the condition to be true.

The condition (3<2 or 1<3 or 4<2) is true since since the middle smaller expressions is true.

In fact, the only way for the condition to be false is if all of the smaller expressions are false, as in the condition 3 < 2 or 3 < 1 or 4 < 2.

The condition (3<2 or 3<1 or 4<2) is false since since the all smaller expressions are false.

Combining expressions using and and or

Here is a summary of the examples we've considered.

We've seen that a condition using and is True when all smaller expressions are True. Consequently,

it is True only when all smaller expressions are True and
it is False if even one smaller expression is False.

For a condition using or, the condition is True when at least one smaller expression is True. Consequently,

it is False only when all smaller expressions are False and
it is True if even one smaller expression is True.