Branching (Part 1)
Rules for Pig Latin
Now that we know how to write conditions, we can start writing programs that branch, that is, that execute different instructions depending on whether a condition is true or false. Consider, for example, how to translate words into Pig Latin. For example, "How are you?" in English translates to "Owhay areway ouyay?" in Pig Latin.
Exactly what rules you learned will depend on where you grew up. There possible rules are given below:
- Moving a consonant to the end of the word and adding the sound "ay".
For example, "carrot" translates to "arrot" + "c" + "ay". - Moving all consonants up to the first vowel.
For example, "cheese" translates to "eese" + "ch" + "ay". - Applying a special rule for words starting with vowels.
For example, "apple" translates to "apple" + "w" + "ay".
Any time you encounter a situation where there are different possible cases, the technique to use is branching. In other words, the application of different actions for different cases is called branching.
Branching in a program
Computer scientists have a not-quite accurate view of the natural world. It is true that when you climb a tree, choosing a branch is choosing a direction to climb. But in a program, it is as if branches could rejoin later on.

Branching is like climbing a tree:
We choose a direction (branch).
Image: robodread/iStock/Thinkstock

Branching is unlike climbing a tree:
Branches can rejoin later.
Image: theospoint/iStock/Thinkstock
Applying a discount
Let's look at the example of a discount for seniors. Here we have two possible courses of action: we can either apply a discount or do nothing. So applying a discount and doing nothing can be viewed as two branches:
- Branch 1: If the customer is at least 65 years old, apply a discount.
- Branch 2: Otherwise, do nothing.
If in both situations we add the tax and return the total bill, it is as if the branches rejoined: our tasks differ for a while, but then become the same. How do we make a choice between the two courses of actions? As when we discussed booleans, we can first think of a question we would want to ask, and then convert it into a statement. What course of action we take depends on whether the statement is true or false:
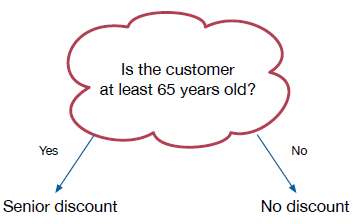
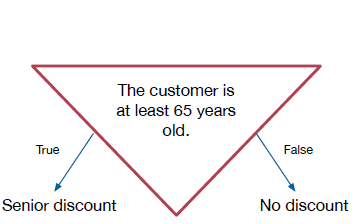
Visualizing branching
Consider the figure (1)-(3) below. As in our earlier pictures, the red circles represent instructions. This time we have a red triangle, which represents a statement, and blue dashed circles, which represent instructions that might not be executed. In each of the figures, there are three red circles, followed by a red triangle, two blue dashed circles, and two red circles.
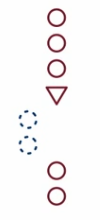
Fig. (1)

Fig. (2)
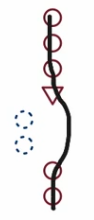
Fig. (3)
If the statement is true, the order of steps goes through the upper red circles, the statement, the blue dashed circles, and then the lower red circles, as shown in figure (2). But if the statement is false, the order of steps goes through the upper red circles, the statement, and the lower red circles without going through the blue dashed circles, as shown in figure (3).
Unused instructions
Some instructions are not used in some cases. This is different from what we have seen up until now. We can write a program which has unused instructions, that is, instructions that are not used in all cases. In fact, if the statement is always false, then the instructions are never used. It doesn't make a whole lot of sense to write a program in that way.
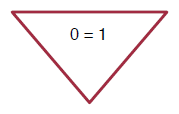
The statement "1=0" is always false because neither 0 nor 1 ever change. In the customer discount example, different customers have different ages, so different situations could occur.
Two courses of action
In our example, there were two courses of action before adding the tax and computing the final bill: either we did something (that is, apply a discount) or we did nothing. This is shown in figure (4).

Fig. (4)
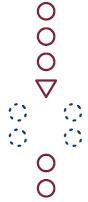
Fig. (5)
In finding the minimum of two numbers, again there are two courses of action. In both courses of action, we do something, as shown in figure (5). Here there are two sets of instructions, namely, return the first number and return the second number. In each case, we execute exactly one of the two sets of instructions.
Visualizing two sets of instructions
In each of the figures below, there are three red circles, followed by a triangle, two dashed blue circles on left and right side after the red triangle, and two red circles.
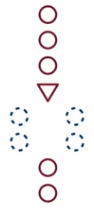
Fig. (6)
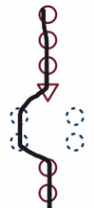
Fig. (7)
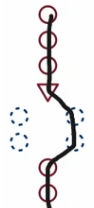
Fig. (8)
The blue dashed circles on the left are to be executed if the statement is true, as shown in figure (7), and the blue dashed circles on the right are to be executed if the statement is false, as shown in figure (8). The sequence of steps for when the statement is true is just like in the earlier example, but now when the statement is false, the blue dashed steps on the right are executed before the lower red circles.
Pseudocode for one set of instructions
How might we translate these into pseudocode? In this pseudocode, we use upper red, blue dashed, and lower red to each represent one or more steps. The line if condition comes after the upper red steps and indicates that the indented blue steps are executed only if the condition is true. Finally, the lower red steps are executed.

upper red if condition blue dashed lower red
As in the visualization, the upper and lower red steps are always executed, but the blue dashed steps are only executed if the statement is true:
- blue dashed circles are executed only if the condition is true, and
- upper red and lower red circles are always executed.
In this function, there are no upper red steps. The condition compares the value of age and the number 65. If the condition is true, that is, age is at least 65, the price is multiplied by 0.9. This is the blue dashed step. If the condition is false, then that step is skipped. In both cases, the tax is added in and the total price returned. These are the lower red steps. The pseudocode is given below:
define discount(age, price) if age >= 65 price ← .9 $*$ price price ← price * 1.13 return price
Pseudocode for two sets of instructions
To translate our second visualization to pseudocode, again we use if to introduce the condition, and we introduce a new keyword, else, to separate the left blue dashed steps and the right blue dashed steps.

upper red if condition left blue dashed else right blue dashed lower red
The left blue dashed steps are executed only when the condition is true and the right blue dashed steps only when the condition is false. Since a condition has to be true or false, exactly one of the sets of steps will be executed. As before, the upper and lower red steps are executed in all cases. In summary,
- left blue dashed is executed if the condition is true,
- right blue dashed is executed if the condition is false, and
- upper red and lower red are always executed.
Here the left blue dashed steps consist of assigning first to the variable minimum and the right blue dashed steps" consist of assigning second to the variable minimum. Exactly one will be executed. Notice that if first and second are equal, returning either one would give the correct answer. This example has print(minimum) as the lower red steps. There are no upper red steps.
The pseudocode is given below:
if first <= second minimum ← first else minimum ← second print(minimum)
As our examples get more complex, like in this case, I'll be using parts of programs instead of complete programs or complete functions. A code fragment may be incomplete. In a fragment like this, you can assume that first and second have both been defined before this code is executed.
 Python from scratch
Python from scratch