Recursion (Part 2)

Recursive calls without end

When we traced our factorial function, we discovered that the calls would never end:

To determine fact(4), we multiply 4 by fact(3): fact(4) ⇒ 4 * fact(3)

This in turn has the value of 3 multiplied by fact(2): 4 * fact(3) ⇒ 4 * 3 * fact(2)

Using the function again, fact(2) is replaced by 2 times fact(1): 4 * 3 * fact(2) ⇒ 4 * 3 * 2 * fact(1)

This is replaced by 1 times fact(0): 4 * 3 * 2 * fact(1) ⇒ 4 * 3 * 2 * 1 * fact(0)

This is now replaced by 0 times fact(-1): 4 * 3 * 2 * 1 * fact(0) ⇒ 4 * 3 * 2 * 1 * 0 * fact(-1)

This is replaced by -1 times fact(-2): 4 * 3 * 2 * 1 * 0 * fact(-1) ⇒ 4 * 3 * 2 * 1 * 0 * -1 * fact(-2)

As you can see, this process does not end.

Recursive calls that end

We want for the calls to end so that we can return a value.

Visualization 1

Again, let's represent each function call using a rectangle and a function call from inside the fuction by a circle within this rectangle.

As before, we call fact(4), which in turn calls fact(3) :

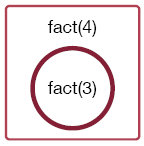
A call to fact(3) results in a call to fact(2):

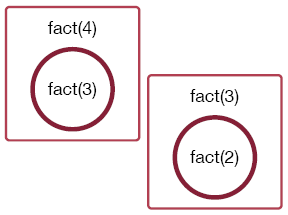
This results in a call to fact(1), which does not call the function again.

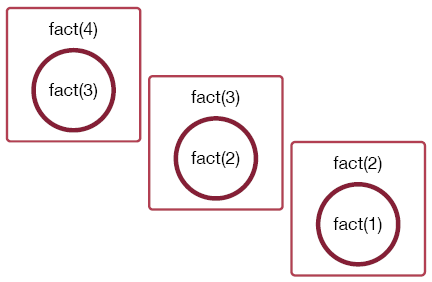
We don't multiply by zero, we don't go on forever we just return the value of fact(1), which is 1. This allows the other function calls to complete.

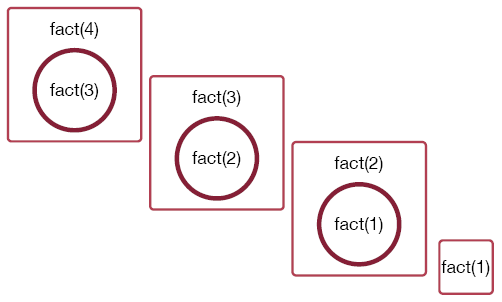
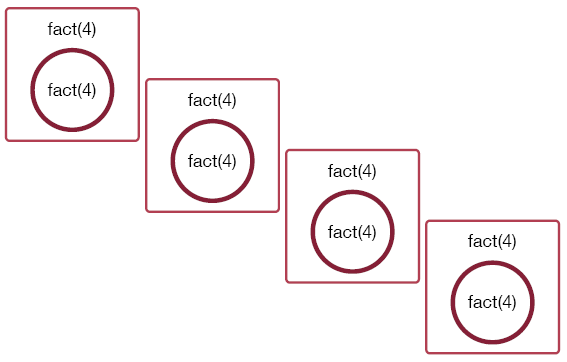
Visualization 2

Using our other visualization, again, let's use circles for steps and a bigger circle for a function call. We represent each factorial function as consisting of two initial steps before the the function call and another two steps after the function call. Using circles, this is represented by two red circles, followed by a bigger red circle and two red circles.

Don't worry about the exact number of steps - this is just to give you an idea of how the function calls work. The steps in the first function call are executed until a function call is reached.

Then the steps in the second function call are executed until a function call is reached.

Then the steps in the third function call are executed until a function call is reached.

But then in the fourth function call, there is no further function call. So the fourth function call can be completed.

Then the fourth function call returns a value to the third function call.

Then, the third function call can be completed and returns a value to the second function call.

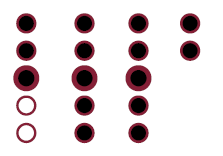
Then, the first function call can be completed.

Base cases

The type of function we are writing is called a recursive function. We also say that the function uses recursion.

This means that there is at least one case in which there is a recursive call used. What was missing from our function was a base case, that is, a case in which the problem can be solved without using the function yet again. Without a base case, the sequence of function calls never ends.

Whenever you write a recursive function, make sure you have at least one of each type of case.

Fixing the factorial function

We can fix our function by keeping the recursive case and adding a base case. define fact(num) if num == 1 return 1 else return num * fact(num-1)

We check if num equals 1 and if so return 1 without calling fact again. Initially, the trace looks like the earlier one. Let's examine a trace. fact(4) ⇒ 4 * fact(3) ⇒ 4 * 3 * fact(2) ⇒ 4 * 3 * 2 * fact(1) ⇒ 4 * 3 * 2 * 1 ⇒ 4 * 3 * 2 ⇒ 4 * 6 ⇒ 24

We keep using the recursive case to make a call until we reach fact(1). Then we can return the value 1, which gets multiplied by the 2 in the call to fact(2), resulting in 2, which in turns gets multiplied by the 3 in the call to fact(3), resulting in 6, which in turn gets multiplied by the 4 in the call to fact(4), resulting in the return of value 24, the factorial of 4.

More pitfalls

This isn't the only danger in using recursion. Suppose we had accidentally called fact(num) instead of num-1 in the recursive case. Then, a call to fact(4) results in a call to fact(4). This results in a call to fact(4) again. You can see where this is going.

In order for the calls to end, you have to be able to reach the base case. That happens by making sure that the input to a recursive call is closer to a base case than the input to the original function. I used “a recursive call” and “a base case” instead of “the recursive call” and “the base case” as there could be more than one of each.

Using recursion safely

Just like mutation, recursion is handy, but dangerous. Following this sequence of steps should help.

First, make sure that the call is on an input closer to a base case, which is only useful if there actually is a base case. There should be at least one recursive case, and any possible input should be covered by one of the base cases or one of the recursive cases.

---